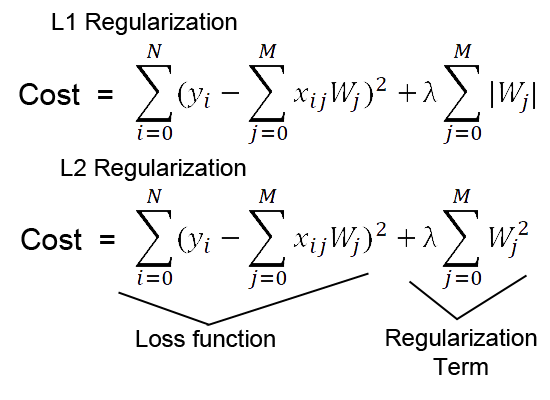L1 VS L2 regularization

Regularization will help select a midpoint between the first scenario of high bias and the later scenario of high variance.
This ideal goal of generalization in terms of bias and variance is a low bias and a low variance which is near impossible or difficult to achieve.

L1

• lambda of the summation of the absolute value of the coefficients.

• tries to estimate the median of the data
  • can handle high dimensional data
  • no need for feature selection

• helps to reduce the overfitting in the model as well as feature selection.

• sparse, and important feature selection

• helps in feature selection by eliminating the features that are not important.
  • penalizes features that have low predictive outcomes by shrinking their coefficients closer to zero.

• can be used for classification or regression

• use case:
  • predicting housing prices
  • predicting clinical outcomes based on health data

L2

• lambda of the summation of squared coefficients.

• reduces the complexity of the model by shrinking the coefficients.

• estimate the mean of the data

• helpful when the number of feature points are large in number

• helpful when data suffer from multicollinearity

• helps in feature selection by eliminating the features that are not important.
  • penalizes features that have low predictive outcomes by shrinking their coefficients closer to zero.

• can be used for classification or regression

• use case:
  • predictive maintenance for automobiles
  • sales revenue prediction

L1 and L2 regularization are common techniques used in machine learning to prevent overfitting by adding a penalty term to the loss function. They are particularly popular in linear models like linear regression and logistic regression, but they can also be applied to other types of models.

L1 Regularization (Lasso Regression):

L1 regularization adds a penalty term to the loss function that is proportional to the absolute value of the coefficients:

$\text{L1 penalty} = \lambda \sum_{i=1}^{n} |w_i|$

where:

• \(w_i\) are the model coefficients (weights),

• \(\lambda\) is the regularization parameter that controls the strength of regularization.

L1 regularization encourages sparsity in the model, meaning it tends to force the weights of less important features to zero, effectively performing feature selection.

L2 Regularization (Ridge Regression):

L2 regularization adds a penalty term to the loss function that is proportional to the square of the magnitude of the coefficients:

$\text{L2 penalty} = \lambda \sum_{i=1}^{n} w_i^2$

where:

• \(w_i\) are the model coefficients,

• \(\lambda\) is the regularization parameter.

L2 regularization penalizes large coefficients, encouraging them to be small. It doesn't usually force coefficients to exactly zero, but it can significantly reduce their values, effectively reducing the model's complexity and making it more robust to outliers in the data.

Key Differences:

1. Effect on Coefficients:
   • L1 regularization can lead to sparse models with many coefficients set to zero.
   • L2 regularization shrinks the coefficients towards zero but rarely forces them to zero.

2. Robustness to Outliers:
   • L1 regularization is generally more robust to outliers because it doesn't penalize large individual weights as much as L2 regularization.

3. Feature Selection:
   • L1 regularization performs feature selection by forcing less important features to zero.
   • L2 regularization doesn't perform feature selection as aggressively as L1 regularization.

Choose L1 regularization (Lasso) when:

1. Feature Selection: You want to perform feature selection and prefer a sparse model with only a subset of the most important features. L1 regularization tends to set less important features' coefficients to zero, effectively performing automatic feature selection.

2. Interpretability: You need a model that is easy to interpret and want to identify the most influential predictors in your model.

3. Outlier Handling: Your dataset contains outliers, and you want the regularization technique to be robust to outliers. L1 regularization can be more robust to outliers due to its ability to shrink less important features' coefficients to zero.

4. Reducing Overfitting: You suspect that your model is overfitting and want to reduce the complexity of the model by encouraging sparsity in the coefficients.

Choose L2 regularization (Ridge) when:

1. No Feature Selection Needed: You do not need feature selection or prefer to keep all features in the model. L2 regularization penalizes all coefficients uniformly without setting any of them to zero.

2. Robustness to Collinearity: Your dataset contains highly correlated features, and you want the regularization technique to be robust to multicollinearity. L2 regularization can help stabilize the model's coefficients when dealing with multicollinearity.

3. Handling Large Weights: You want the regularization technique to handle large individual weights more gently. L2 regularization tends to shrink large weights more gradually compared to L1 regularization.

4. Reducing Variance: You suspect that your model is suffering from high variance (overfitting) and want to reduce the model's complexity without eliminating any features entirely.

In practice, you may experiment with both L1 and L2 regularization and choose the one that yields the best performance on your validation or test dataset. Additionally, techniques such as Elastic Net regularization combine L1 and L2 penalties to leverage the benefits of both regularization techniques.

$\text{Elastic Net Penalty} = \alpha \times \text{L1 Penalty} + (1 - \alpha) \times \text{L2 Penalty}$

Elastic Net regularization is commonly used in linear regression, logistic regression, and other machine learning models where regularization is necessary to prevent overfitting and improve model generalization.

Python Implementation (using scikit-learn):

from sklearn.linear_model import Lasso, Ridge
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

# Load sample dataset (Boston housing dataset)
boston = load_boston()
X, y = boston.data, boston.target

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Create Lasso (L1) regression model
lasso = Lasso(alpha=0.1)  # alpha is the regularization parameter (lambda)
lasso.fit(X_train, y_train)

# Create Ridge (L2) regression model
ridge = Ridge(alpha=0.1)  # alpha is the regularization parameter (lambda)
ridge.fit(X_train, y_train)

# Make predictions
y_pred_lasso = lasso.predict(X_test)
y_pred_ridge = ridge.predict(X_test)

# Evaluate performance (e.g., Mean Squared Error)
mse_lasso = mean_squared_error(y_test, y_pred_lasso)
mse_ridge = mean_squared_error(y_test, y_pred_ridge)

print("Lasso Regression MSE:", mse_lasso)
print("Ridge Regression MSE:", mse_ridge)

In this example, we use Lasso (L1) and Ridge (L2) regression models to predict housing prices on the Boston housing dataset. We then evaluate the performance of the models using mean squared error (MSE).

Sparse: If the original derivative is not 0, then the derivative is still 0 after applying L2, so the optimal w will not become 0. When applying L1, as long as the coefficient lambda of the regularization term is larger than the absolute value of the derivative of the original cost function at point 0, w = 0 will become a minimum point.