KNN

The k-nearest neighbors (KNN) algorithm is a simple, non-parametric, lazy learning algorithm used for classification and regression tasks. It works on the principle of finding the 'k' nearest data points in the feature space to the given query point and making predictions based on the majority class (for classification) or the average (for regression) of their labels.

Equation (for classification):

For classification, the predicted class of a query point is determined by a majority vote among its k-nearest neighbors:

$\hat{y} = \text{argmax} \left( \sum_{i=1}^{k} \mathbb{1}(y_i = c) \right)$

Where:

• $\hat{y}$ is the predicted class of the query point.

• $y_i$ is the class label of the \(i\)-th neighbor.

• c represents each unique class label.

• $\mathbb{1}(\cdot)$ is the indicator function, returning 1 if its argument is true and 0 otherwise.

Equation (for regression):

For regression, the predicted value of a query point is the average of the labels of its k-nearest neighbors:

$\hat{y} = \frac{1}{k} \sum_{i=1}^{k} y_i$

Where:

• $(\hat{y}$) is the predicted value of the query point.

• $(y_i)$ is the label of the ith neighbor.

Example:

Suppose we have a dataset with two features (e.g., height and weight) and two classes (e.g., 'cat' and 'dog'). To predict the class of a new data point, KNN finds the 'k' nearest neighbors based on the Euclidean distance and assigns the class label by majority voting among these neighbors.

Python Implementation:

from sklearn.neighbors import KNeighborsClassifier

# Create KNN classifier
knn = KNeighborsClassifier(n_neighbors=5)

# Train the model
knn.fit(X_train, y_train)

# Predictions
y_pred = knn.predict(X_test)

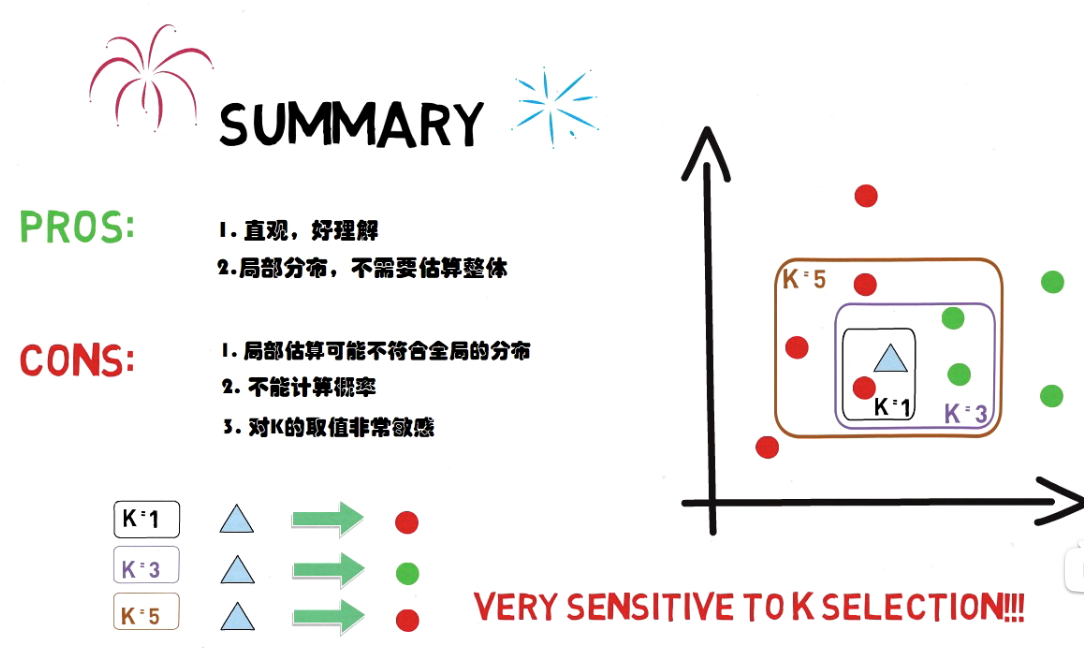
Pros and Cons:

• Pros:
  • Simple to understand and implement.
  • No training phase; the model directly uses the training data for predictions.
  • Works well with multi-class data.
  • Robust to noisy training data and irrelevant features.

• Cons:
  • Computationally expensive during prediction, especially for large datasets.
  • Sensitive to the choice of the distance metric and the value of 'k'.
  • Requires a sufficient amount of training data to produce accurate results.
  • Not suitable for high-dimensional data due to the curse of dimensionality.

Applications:

• Classification problems with relatively small to moderate-sized datasets.

• Recommender systems, such as recommending products or movies based on user preferences.

• Handwritten digit recognition.

• Medical diagnosis.

• Anomaly detection in credit card transactions or network traffic.

KNN is a versatile algorithm that can be applied to various types of problems, but it's essential to understand its strengths, weaknesses, and appropriate use cases.