K-means

Pros:

K-means clustering algorithm of Machine Learning fails to give good results when the data contains outliers, the density spread of data points across the data space is different, and when the data points with non-convex shapes.

k means with single-linked agglomerative method. It is actually creating very small clusters and they based on distance between two closest data points, two clusters are selected which are closest to each other and merged. This is usually beneficial in 'banana shaped' data points.

In which cases will K-Means clustering fail?

Data points with :

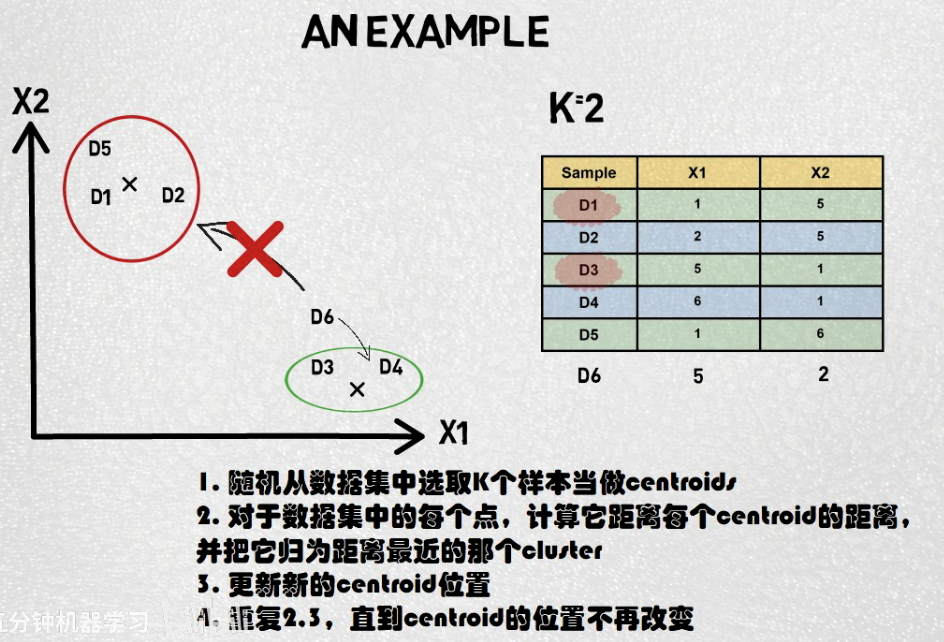
K-means clustering is a popular unsupervised machine learning algorithm used for partitioning a dataset into K distinct, non-overlapping clusters. It is widely used for clustering analysis in various fields, such as image segmentation, customer segmentation, and document clustering.

How K-means Works:

1. Initialization: Choose K initial cluster centroids randomly from the data points or using some heuristics.

2. Assign Data Points to Nearest Centroid: Assign each data point to the nearest centroid based on some distance metric, commonly the Euclidean distance.

3. Update Centroids: Recalculate the centroids of the clusters based on the mean of all data points assigned to each cluster.

4. Repeat: Repeat steps 2 and 3 until convergence, i.e., when the centroids no longer change significantly or the maximum number of iterations is reached.

5. Convergence Criteria: Convergence can be determined by checking if the centroids stop changing or if a maximum number of iterations is reached.

Objective Function:

The objective of K-means clustering is to minimize the within-cluster sum of squared distances (WCSS), also known as inertia:

$\text{WCSS} = \sum_{i=1}^{K} \sum_{x \in C_i} ||x - \mu_i||^2$

where:

• \(K\) is the number of clusters,

• \(C_i\) is the set of data points assigned to cluster \(i\),

• \(\mu_i\) is the centroid of cluster \(i\),

• \(||x - \mu_i||^2\) is the squared Euclidean distance between data point \(x\) and centroid \(\mu_i\).

Choosing the Number of Clusters (K):

Choosing the appropriate number of clusters is a crucial step in K-means clustering. Common approaches include the elbow method, silhouette method, and cross-validation.

1. Elbow Method: Plot the WCSS for different values of K and look for the "elbow" point where the rate of decrease sharply changes.

2. Silhouette Method: Compute the silhouette score for different values of K and choose the value that maximizes the silhouette score.

Python Implementation (using scikit-learn):

from sklearn.cluster import KMeans
import numpy as np

# Generate some sample data
X = np.random.rand(100, 2)

# Create a KMeans instance
kmeans = KMeans(n_clusters=3)

# Fit the model to the data
kmeans.fit(X)

# Get cluster centroids
centroids = kmeans.cluster_centers_

# Get cluster labels for each data point
labels = kmeans.labels_

In this example, we generate some random 2-dimensional data points and perform K-means clustering with 3 clusters. We then obtain the cluster centroids and labels assigned to each data point.

Pros and Cons of K-means:

Pros:

• Simple and easy to implement.

• Fast and efficient for large datasets.

• Scales well to high-dimensional data.

• Often gives meaningful results when the data is well-separated.

Cons:

• Requires the number of clusters (K) to be specified in advance.

• Sensitive to the initial choice of centroids, which can lead to different results for different initializations.

• May converge to a local minimum, especially when the clusters have varying sizes, densities, or non-spherical shapes.

• Assumes clusters are spherical and isotropic in shape.

K-means is a powerful and widely-used clustering algorithm, but it's important to understand its limitations and consider alternative methods for more complex clustering tasks.

import numpy as np

class KMeans:
    def __init__(self, n_clusters, max_iter=300):
        self.n_clusters = n_clusters
        self.max_iter = max_iter

    def fit(self, X):
        # Initialize centroids randomly
        self.centroids = X[np.random.choice(X.shape[0], self.n_clusters, replace=False)]
        
        for _ in range(self.max_iter):
            # Assign each data point to the nearest centroid
            labels = np.argmin(np.linalg.norm(X[:, None] - self.centroids, axis=2), axis=1)
            
            # Update centroids
            new_centroids = np.array([X[labels == k].mean(axis=0) for k in range(self.n_clusters)])
            
            # Check for convergence
            if np.allclose(new_centroids, self.centroids):
                break
                
            self.centroids = new_centroids

    def predict(self, X):
        return np.argmin(np.linalg.norm(X[:, None] - self.centroids, axis=2), axis=1)

# Example usage
# Assuming X is your dataset

kmeans = KMeans(n_clusters=3)
kmeans.fit(X)
labels = kmeans.predict(X)